Geometry optimization

grasshopper
1

Hello there
I want to optimization with galapagos,
My subject is Geometry optimization to reduce heating &cooling & increase daylight.
But the result is not convergent
What is the problem?
It’s about to optimize the length and with of the rectangle.

IMG_20200903_154838_554
IMG_20200903_154838_5541280×696 186 KB

2

Hi -

Without your Grasshopper definition, that’s impossible to say.
-wim

3

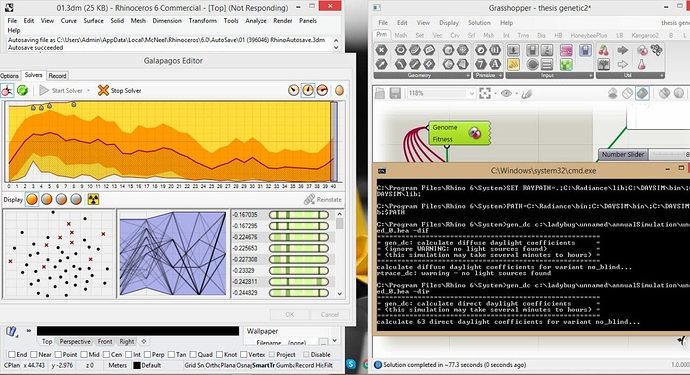
No, with honeybee ladybug but my problem is convergent
I send a photo
I want to know is it true but ignore negative of result

4

I’m afraid that 1000 photo’s are still less informative than the .gh file…
-wim

5

As far as I know you cant use the galapagos for multi-objective optimization, it can be used for single objectives. You can try to use octopus maybe thats the problem

6

Hi -

That’s correct but you can often combine multiple objectives into one single value to be maximized / minimized.
-wim

1 Like
7

@Qodsiye

I agree with @wim re: gh file. In addition I can provide some advice on building effective search/optimization algorithms in general. Specifically, I think there are a couple of common mistakes you could look into:

  • Standardize or scale your input/output data. The range of heating/cooling values (in Wh, kWh/m2 etc) will be significantly different from whatever you choose for your daylighting metric, which will bias your results to the inputs/outputs with larger magnitudes. For optimization problems you generally want to scale all your dataset between 0 and 1 to avoid this (sometimes referred to as min-max scaling). In certain cases you may want to standardize your data, which means subtracting the data by it’s mean value, and dividing by it’s standard deviation, so all your data has the same (unit) standard deviation. Standardization is useful in cases where the distribution of data is more important then the scale of it’s range. For your particular problem, I recommend scaling your output data, if you haven’t already.

  • Sufficiently small increment steps. If the change in your input data (length/width) is too large, the GA optimization may be overstepping the local minimas/maximas in your fitness search space, which means it never converges to a solution. So you should systematically vary your increment steps to find one that produces the best solution.

  • Similarly, you need to construct your single-objective optimization function to provide a meaningful output “gradient” so that there is a minimum or maximum point to find. This is partially addressed by scaling/standardizing your data, but some of it will just be intrinsic to the problem domain. For example if you weight your scaled daylighting and heating/cooling outputs equally, there will be a fitness trade-off between increase in daylight and decrease in thermal, which may result in the same output value for multiple inputs. This will not provide a meaningful gradient for the GA to search through. This is a problem that is going to arise with highly correlated outputs (which daylighting and heating/cooling is) which brings me to my next point…

  • Highly correlated data. You want your inputs to have a high correlation (the degree to which one dataset can predict another) with your output data, but you don’t want your inputs to be highly correlated with eachother, or your outputs to be highly correlated with eachother. This kind of high correlation increases the entropy/randomness of your output, since there isn’t a clear relationship between changing one parameter or the other. The higher the randomness, the harder it is for the GA to identify a slope or direction from the information you feed it. In your case, your inputs aren’t correlated (in fact they have a correlation of 0), but your outputs are, (as mentioned in the previous point), so you should weight the results so there’s a bias/direction in your single objective function.

S

2 Likes