Ladybug Wind Rose # of arrows - only use _numOfDirections of 36 or 12

[LelandCurtis]

Ladybug Community,

I just realized all of my windroses have an error. I like to use roses with 16 cardinal directions, which seems to be the WindRose default. But wind direction data is stored in 10 degree increments. This means if you plot this data using any number of arrows that are not a divisor of 36, it will unevenly distribute data. See images below.

Plotting the data on 36 arrows, you see that the colored circles represent true values.

Plotting the data on 16 arrows overemphasizes the 270 degree arrow.

Looking closer, you’ll see that is because three buckets of data (280, 270, 260) are filling this arrow, while only 2 buckets of data (250, 240) are filling the other.

18 directions also has issues as shown below.

12 works but is a bit imprecise.

@mostapha, @chris, should the Ladybug Windrose be updated to only accept _numOfDirections values that are divisors of 36? At a minimum it would be nice to update the default _numOfDirections from 16 to 12.

The good news is that this only shifts the graphic slightly and most conclusions drawn from the roses will remain the same. So I don’t want to freak anyone out. Still, I’m going to update my windroses and encourage the community to do the same.

[SaeranVasanthakumar]

@LelandCurtis

You’re right that the number of directions of the windrose does skew the resulting frequency due to the wind direction interval. And I like the idea of setting the default to 18, to force angle intervals of 20. However I don’t think it’s an error, and we shouldn’t try to constraint the division intervals based on the wind data sampling.

I’m the one who wrote the latest windrose component, and when I did, the underlying idea was to more explicitly treat the windrose as a stacked histogram (an approximation of the distribution of data binned by user-defined intervals).

I think it’s a lot more useful to make the conceptual leap of thinking of the windrose explicitly as a histogram, because we can bring the tools and methods from statistical analysis to interpreting the windrose. In this case you’ve identified the common problem in histograms of the bin interval skewing the resulting frequency distribution. I think the best solution is to make the bin intervals smaller to get a better idea of the underlying sample. This is something Andrew Gelman (statistics prof) has written about before: https://statmodeling.stat.columbia.edu/2009/10/23/variations_on_t/. He makes the point that “the jaggedness of a slightly undersmoothed histogram performs a useful service by visually indicating sampling variability,” and thus supports really thin bin intervals.

So I think the solution is to just encourage more robust, statistical thinking about extrapolating a representation of data to represent its underlying population. This preserves all the usefulness of the underlying histogram logic (i.e if someone wanted to fit a probability density function to the wind data, they could do it with the histogram that is computed by this component). Another advantage is that the tool is more flexible that way, and not tied to a single type of direction interval. For example, what if someone wanted to bring in wind data at finer intervals (i.e from some CFD for example).

S

[LelandCurtis]

@SaeranVasanthakumar, first of all, thank you for your work on the windrose. I love this component!

I agree that this isn’t an error in the sense that the windrose is working perfectly as a histogram. However, so long as the primary use of this component for the vast majority of users is to display 10-degree EPW wind data, this setting is an invitation to make mistakes. Any windrose using something other than 36 or 12 bins to display standard EPW wind data is improperly binned, and the community should be made aware of this. Even 18 bins appears problematic, as half the values land directly between two bins.

I like your approach of keeping the windrose as a generic radial histogram and see how my recommendation to constrains the bin setting would prevent this. So how do we preserve the histogram logic while avoiding errors in the primary use case?

It seems we agree the obvious solution is to change the default settings so that the standard use case is properly binned. That solves 95% of the problem. 12 seems too rough, so I’d probably go with 36. I don’t see how to enable 18 without rotating, which would interfere with the histogram logic. I’m curious what most users prefer.

I think it would be helpful to add a hint in the _numOfDirections input to warn users how stepped data like the EPW wind direction is susceptible to improper binning. If this was a rare case on custom data expecting users to show more robust statistical thinking makes. But as long as the primary use case of the wind rose is to display EPW wind data, I worry this parameter will encourage mistakes. A warning would go a long way.

[SaeranVasanthakumar]

@LelandCurtis

I think 36 works, it’ll center the EPW directions nicely and having thinner bins is consistent with Gelman’s suggestion. And then there can be a comment explaining why the number is chosen.

[chris]

Yes, all credit for the new wind rose goes to @SaeranVasanthakumar , including both the beauty of it and the performance!

Changing the component default sounds reasonable but I think we also need to bear in mind that not all EPW data is equal. I know that a lot of EPWs in the US have wind direction reporting increments of 10 degrees but this is not a fundamental rule of EPWs and you can definitely have EPWs with finer wind directions (eg. 273 degrees or something like that).

Conversely, some EPW files have wind data at coarser intervals like 20 degrees. For example, if we made 36 the default number of directions, this is what the SWERA Beijing weather file would look like by default:

So, before we pick a default value that might be a bit biased towards the EPWs that we work with most, we should test a few different files from around the world or at least test some different EPW sources. My intuition tells me that 18 might work best for most EPWs from around the world. But we might want to consider 12 if we find some EPWs only report wind directions in increments of 30 degrees.

[LelandCurtis]

Hmm, that complicates things.

Is there a way to provide a test/warning within the component itself? For example:

• test the input data to identify if the data is stepped, and if so, at what interval
• Compare data step against chosen bin interval
• throw a warning if they are out of line

This wouldn’t have to cover all use cases, but could be targeted to solve the common EPW wind data issues we are discussing.

In fact, if _numDirections input is empty (default is being used) perhaps this default value could be updated automatically based on this test. Users could always force their binning by inputting a value, allowing the histogram to function flexibly while helping users get accurate wind roses from a variety of EPW data sources. Is that adding too much complexity?

[SaeranVasanthakumar]

@LelandCurtis, @chris

That’s right, there are non-10 degree wind intervals in EPW files! Thank you for reminding me Chris, this is one of those facts that I always learn, and then promptly forget for some reason.

As for a strategy of accommodating such intervals, I would argue that we are going about this the wrong way. Right now we are debating (a) trying to find a common factor for some common subset of EPW intervals or (b) adding a series of tests to check bin intervals. In the first case, that common factor may not exist, and we are accepting it will be broken by custom or exotic datasets. For the second option I suspect the logic we’d be using to try and identify which bin intervals are inappropriate will have to be very convoluted to account for all possible scenarios, and still might be brittle.

Specifically, we falling into the dilemma captured by Anscombe’s quartet. Anscombe’s quartet illustrates four datasets that have identical descriptive statistics, but differ greatly when graphed. Here’s a modern example of Anscombe’s quartet called ‘The Datasaurus Dozen’, which illustrates the same average, deviation, and correlation with widely varying datasets:

Anscombe quartet illustrates the importance of visualizing data (especially data prone to outliers) before analyzing it numerically. That’s why every statistical workflow starts with visualizing data, even for extremely high-dimensional data (using methods to project the data down to 2 dimensions for visualization like t-SNE or PCA).

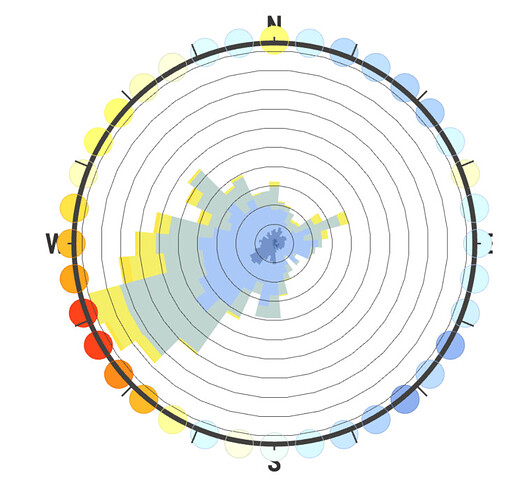
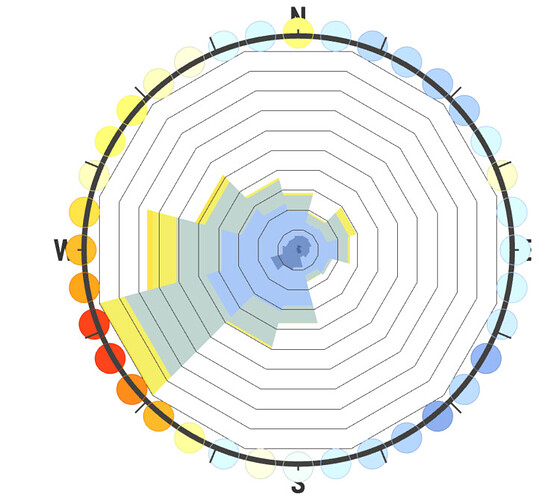
So I would argue we are ignoring the effectiveness of just plain data visualization by a human to identify the skewing of the windroses based on poorly-chosen intervals. And that’s why I think the use of 36 bins is our best option, because it’s so thin it most clearly illustrates the underlying distribution of the EPW sample, and users can then modify the interval number as they wish to approximate the weather population (sample being a rough measurement of reality which in statistics is called a population).

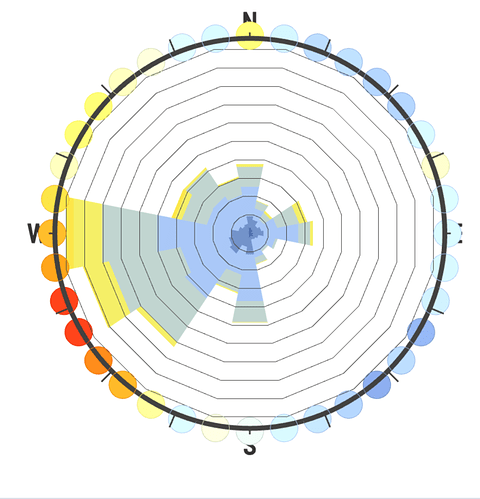
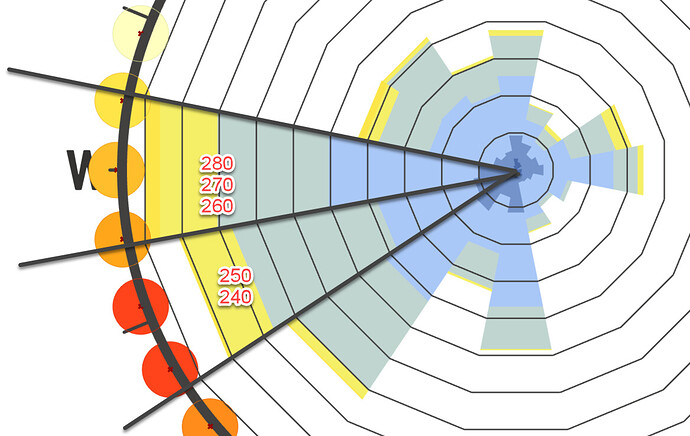
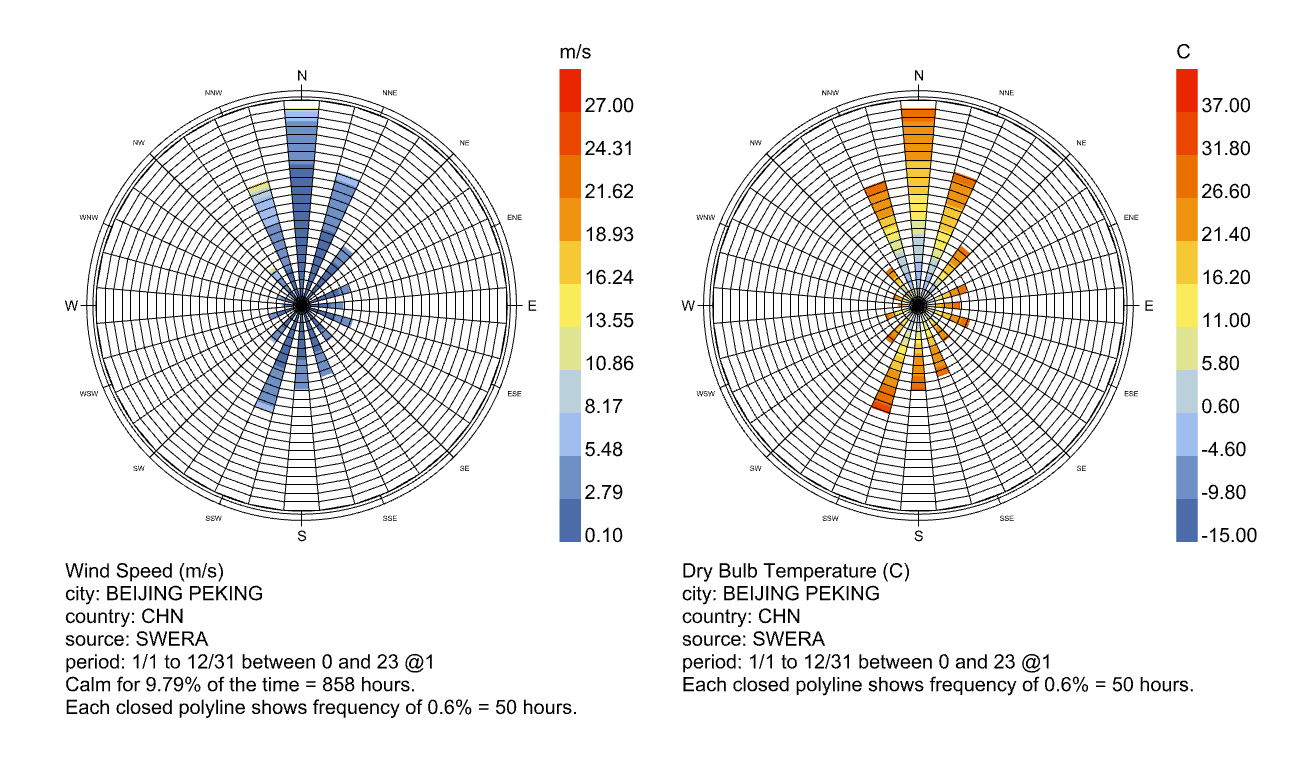
I agree that in the case of the SWERA Beijing file, 36 intervals is “wrong” but it’s actually wrong in a different, more useful way then Leland’s example at the top. That is, it doesn’t mislead us with a slightly rotated set of wind directions by clumping frequencies too broadly, but instead explicitly shows us that the measurement intervals for this dataset are very coarse, and in that way also intuitively implies the solution of increasing the bin interval width to better represent the population distribution.

It’s not perfect, but I think using 36 intervals will actually be the most robust against the kind of user-error we are worried about, versus other numerical methods of capturing skewed direction frequencies due to different sampling intervals. What do you guys think?

[LelandCurtis]

@SaeranVasanthakumar, I think you nailed it.

I like your point that 36 bins will work well for many common EPW datasets, and that when it fails, it fails in a useful, clarifying way. In fact, I think the visual “warning” of a weird looking rose is better than any text warning that pops up in the component. You’ve addressed all my concerns!

[chris]

Alright, I changed the default to 36 for the version 1.2 stable release we have planned for tomorrow. We can always change it back if we find the larger community does not like it.