Surface emissivity in mean radiant temeperature calculation of Microclimate Map Analysis

grasshopper honeybee-legacy
1

Hello,

I am carrying out a research on mean radiant temperature modeling in outdoor settings, and I would like to better understand the calculation procedure implemented in the Microclimate Map Analysis component of Honeybee, as it has been used in recent studies to estimate outdoor Tmrt. I am new to Ladybug tools so I have some questions that I hope you can clarify.

I gathered that the calculation is performed based on a solar adjusted mean radiant temperature, using the ERFsolar model to adjust the longwave Tmrt calculated for the surrounding surfaces and the sky.

I checked some references and the python code of the component and I gathered that the longwave Tmrt from the environmental surfaces is calculated by multiplying the surface view factors and the surface temperature, calculated by Energyplus but, based on my understanding of the formulation, the surface emissivity is not taken into account to calculate the longwave radiation emitted by the surfaces, thus all the surfaces are assumed as black body emitters.
In that case, I guess that changes in surface emissivity would only affect the fraction of longwave radiation absorbed by the surface and therefore the surface temperature calculated by Energyplus (that in the outdoors is also based on the absorbed solar radiation, convective exchanges and conduction, as written here: https://bigladdersoftware.com/epx/docs/8-0/engineering-reference/page-020.html).
Is it right or am I missing something? There is a way to include the emissivity of the surrounding surfaces in the Tmrt calculation?

Thank you in advance!

2

@syltetoy

I checked some references and the python code of the component and I gathered that the longwave Tmrt from the environmental surfaces is calculated by multiplying the surface view factors and the surface temperature, calculated by Energyplus but, based on my understanding of the formulation, the surface emissivity is not taken into account to calculate the longwave radiation emitted by the surfaces, thus all the surfaces are assumed as black body emitters.

EnergyPlus does take into account the emissivity of the environmental surfaces. It says so in the documentation you referenced (if you scroll down to ‘External Longwave Radiation’):

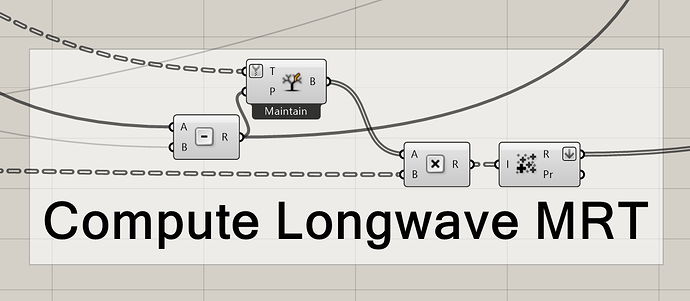
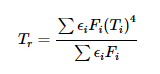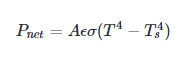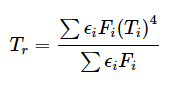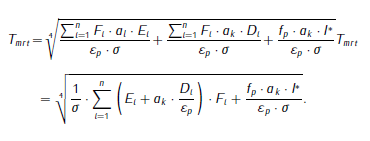image
image785×335 23.1 KB

You can modify the emissivity in Ladybug when you specify the material properties of the surface constructions…or am I misunderstanding your question?

4

@syltetoy

Okay, I think I know what you’re saying. You’re right there is a simplification - the MRT calculation assumes the emittance of all surfaces are very high (close to one) and so typically simplifies the equation to just the summation of the product of view factors and temperatures. However, in cases where the emittance isn’t close to one, your point is that this would be inaccurate. I’ve seen previous instances where emissivity is accounted for by including an area-weighted average of emissivity and the view factor in the calculation, like this equation for MRT from EnergyPlus:

image

Is this formula what you are asking for?

S

ETA: Something I noticed a long time ago, if you look at the formula for the net radiation exchange that is commonly used in introductory physics/building science courses, and do the derivation yourself, you’ll notice the same assumption is made - that the emittance of surroundings is equal to one.

image

5

Yes, that’s exactly what I meant, I am sorry if my question was not clear enough. Thank you!!
I would like to test the effect on different material properties (including low emissivity ones, like metal and glazing) on outdoor Tmrt.
The formulation I would like to use to calculate the longwave Tmrt is the fourth root of the numerator of the formulation you quoted, like this (the third formula):
image
(adapted from this paper)

Do you think there is any way to do it in Honeybee? Like “extracting” surface emissivity values from energyplus and using them in the Tmrt formulation

Thank you!

6

Hey @syltetoy and @SaeranVasanthakumar ,

You are correct that the legacy microclimate maps do not use the emissivity of the various surfaces when calculating longwave MRT at each grid point. But, to be more specific about the assumption that’s being made, the microclimate maps are not assuming surfaces have an emissivity of 1. Rather they are assuming that the emissivity of the surrounding surfaces are all comparable.

Bear in mind that it’s emissivity difference that affects the radiant exchange calculation. Not absolute emissivity. If a person is surrounded by surfaces that all have an emissivity of 0.1, you will have the same longwave MRT for the person if the surfaces all had an emissivity of 0.9. I know that feels bizarre but radiant exchange is weird.

In any case, you are right that the microclimate maps should account for emissivity of different surfaces to make them more accurate and I plan to account for this in the LBT plugin (I’m starting to implement the microclimate maps there now). If you really need to account for emissivity now, you can try to hack the legacy microclimate map component and, if you go down this route, I apologize in advance that my code from 5 years ago is so messy.

Or you can try to do your own long wave MRT analysis using the Ladybug view factor component like this example:

Also, for the record the maps do the calculation with the 4 and 1/4 exponents. You can see the specific lines doing the long wave MRT here:

7

Good point. That makes sense intuitively, but also you can also see that assumption is baked into the formula here:

image

The summation of emissivity and view factor at the bottom is a normalizing constant that converts the all the emissivity view factor products to between 0 and 1, precisely so it’s only the difference that matters.

8

Thank you for the help! I will for sure try to make my own longwave Tmrt based on the example. It is very useful for my analysis, thank you.

I am very happy to hear that you are planning to add emissivity in the new version :slight_smile:

However, I have put some thought into it and I have some doubts with respect to this, so if you don’t mind I would like to deepen it a bit: is it due to longwave reflections?
I mean, lower absorbance/emissivity results in higher reflectivity for longwave radiation and viceversa, so I understand that in an indoor space where shortwave radiation is neglected, in the end the amount of longwave radiation impinging on the human is the same (however I am not sure if that would apply also in outdoor conditions where solar radiation is relevant and influences surface temperature).
Is this what you meant or did you refer to other aspects I am missing?

However, in case it is, it seems to me that the formulation in Honeybee only accounts for the emitted longwave radiation, not the reflected one, and a change in all emissivity values (if added) would result in a change in Tmrt. At that point for formulation would be equivalent to that in my previous message (from the paper).
I have also checked in the ASHRAE Fundamentals Handbook and the Honeybee Tmrt formulation is presented under the assumption that all surfaces are black body emitters.

I think that the Tmrt formulation of Energyplus is for indoor environment and is based on some calculation assumptions (maybe applied to the view factor calculation? – I don’t know). Besides, the results would be expressed in K^4, so honestly I am not really understanding that formulation unless is linearized (as it is suggested on the Energyplus webpage).

Thank you very much for the patience and sorry for the long message!

Syltetoy

9

@syltetoy

However, in case it is, it seems to me that the formulation in Honeybee only accounts for the emitted longwave radiation, not the reflected one, and a change in all emissivity values (if added) would result in a change in Tmrt.

This sounds right, I’ve never seen MRT calculations accounting for reflected long wave radiation, presumably because you’re not usually surrounded by low-emittance materials, and the resulting magnitude of reflected long-wave radiation is so small it’s not worth the extra complexity of calculation (i.e calculating bounces etc).

Besides, the results would be expressed in K^4, so honestly I am not really understanding that formulation unless is linearized (as it is suggested on the Energyplus webpage).

I guess you’re talking about this formula, and the fact that they’re not taking the fourth root of the solution:
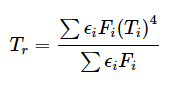
image

I agree, it doesn’t make sense. I think it’s a typo. We can assume all temperatures are taken to the fourth power for the purpose of the discussion, since we’re talking about circumstances where the linear assumption fails (large temperature differences between surfaces). It doesn’t change any of the formulas in a meaningful way (although implementation-wise multiplying really huge numbers by small fractions is a headache when trying to maintain numerical precision).

At that point for formulation would be equivalent to that in my previous message (from the paper). *
I have also checked in the ASHRAE Fundamentals Handbook and the Honeybee Tmrt formulation is presented under the assumption that all surfaces are black body emitters.

I’ve looked over the paper you are referencing. I can see that that this formula:
image

…follows from the paper’s version by limiting to just long-wave, and expanding the E_i term:
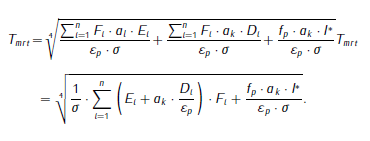
image

The math is correct. However, it is missing the normalizing constant (dividing by the sum of the emissivities and view factors) that all the EnergyPlus MRT calculations incorporate when using angle factors.

I believe this is the case because the formula in the paper you’re referencing assumes the radiation balance includes quantities with larger radiation magnitudes like the diffuse or direct solar components. If you are only looking at long-wave radiation, the associated magnitude is smaller, and you need to normalize the calculation to deal with omissions in the radiation balance (like for example, the long-wave reflections). I could be wrong about this, so correct me if there’s an error in my logic.

But intuitively it makes sense. For example, if you are surrounded by two flat, infinite plates, both with an emissivity of 0.1, and a surface temperature of 29C, your formula would produce an MRT close to zero. If you include the normalization constant, the MRT would be 29C, since the 0.1 emissivity and 0.5 view factor would be normalized to 0.5. In an actual radiation balance, the reflected long-wave radiation would be significant and summed with the (very small) emitted radiation, such that there would be zero radiation exchange between you and your environment (assuming you are also ~29C and have emissivity of ~1), and thus the actual MRT should be close to 29C.

Basically, the normalizing constant ensures that the view-factor and emissivity sums to one, and thus acts like a proper radiation balance, whereas your formula can create situations where the radiation isn’t balanced.

10

That’s a good and very thorough explanation, @SaeranVasanthakumar . And, yes, you are both right that what is lost in the radiation balance from a low-emissivity surface is made up for an increase in longwave reflection.

But, just to clarify what honeybee currently does and what I plan to implement:

  • In Legacy - There is no accounting of emissivity at all in the legacy honeybee thermal maps and we just assume everything is at the same emissivity.
  • In LBT - For the new thermal maps that I am currently working on for the LBT plugin, we will account for emissivity differences but I will do so with a “normalizing term” like Saeran showed and I do not plan to do a whole longwave ray-tracing calculation with reflections. Or at least not by default. Technically, it will be possible to do a longwave reflection calculation if someone is motivated and they want to delve into the source code since the new longwave calculations will be with Radiance, which can do reflections. But doing a full longwave reflection calculation by default is just overkill for typical cases. So the right decision for the community seems to be to not let the edge-case make the mainstream use-case overcomplicated.
11

Thank you @SaeranVasanthakumar for the explanation, it has helped me a lot to better understand the formulation, and thank you @chris for the calculation details. I am looking forward to the new thermal maps then :star_struck:

12

Hi, i’ve been working on validating Honeybee simulation of MRT with field measurements so all the info in your replies is really useful, thanks for that!

I’m just wondering, or possibly overthinking, if energyplus is considering the emissivity of a material’s surface in its surface temperature calculations, which you linked in your previous reply, doesn’t that mean the surface temperature output is actually the radiant temperature? And therefore emissivity doesn’t need to be included in MRT calculations?

Or because the emissivity is assumed to be the same as absorptivity in the surface temp calculations does EnergyPlus add emissivity into the MRT calculation to then give the radiant temperature?

I’m interested in this because i’d like to be able to simulate the effect of low emissivity materials on thermal comfort.

13

Hi @chris
Can i double check with you please - does the HB UTCI component now include emissivity and a normalising factor when calculating the longwave MRT as you’re discussing in the above convo?

I ask because i cant see this in the source code (from here: ladybug_comfort.map.mrt — ladybug comfort documentation)

this bit specifically?

load the EPW and outdoor surface temperatures if they are needed

if enclosure_dict['has_outdoor']:
    if sql_obj is not None:
        out_srf_outp = 'Surface Outside Face Temperature'
        out_srf_dict = {d.header.metadata['Surface']: d for d in
                        sql_obj.data_collections_by_output_name(out_srf_outp)}
        out_srf = [out_srf_dict[s] for s in srf_order[:-3]]
        if out_srf[0].header.analysis_period != a_per:
            out_srf = [d.filter_by_analysis_period(a_per) for d in out_srf]
    else:
        out_srf = []
    epw_obj = EPW(epw)
    out_avg = epw_obj.dry_bulb_temperature
    out_sky = epw_obj.sky_temperature
    if not a_per.is_annual:
        out_avg = out_avg.filter_by_analysis_period(a_per)
        out_sky = out_sky.filter_by_analysis_period(a_per)
    out_data = out_srf + [out_avg, out_sky, out_avg]
    out_data = tuple(zip(*out_data))

# load the view factors and perform the matrix multiplication with temperature
with open(view_factors) as csv_data_file:
    vf_data = tuple(
        tuple(float(val) for val in row.split(',')) for row in csv_data_file)
mrt_data = []
for sen_enc, view_facs in zip(enclosure_dict['sensor_indices'], vf_data):
    if sen_enc == -1:  # outdoor sensor
        temp_data = out_data
    else:  # indoor sensor
        temp_data = in_data[sen_enc]
    sensor_vals = []
    for t_step in temp_data:
        sensor_vals.append(sum(vf * t for vf, t in zip(view_facs, t_step)))
    mrt_data.append(sensor_vals)
return mrt_data

But maybe im not looking at the right document?

14

Thanks for checking the source code, @sineadn . You found the right part of the code, which is here on GitHub:

You’re right that I have not yet implemented any emissivity weighting in the calculation of long wave temperature, even though I said that I would 2-3 years ago.

As you said in November, E+ will account for the emissivity in its calculations of surface temperature but the place where I’m not correctly accounting for it is in the radiant exchange between the “occupant” and the E+ Surface. At the moment, I basically assume that the occupant and the Surface have the same emissivity.

Admittedly, this is a bit far from the top of my agenda since there aren’t too many people studying the effects of low-e materials directly on occupant thermal comfort. But I plan to get to ti eventually and I opened up a GitHub issue to make sure that I do not forget.

15

Thanks for the response. Understandable it’s not high on the list of to do’s! In the end, as a work around for my project, I just added emissivity and the normalisation to the code of the legacy MRT Calculator component to calculate a longwave MRT. Like this:

def getMRT (temperatures, viewFactors, emissivities):
equRight = 0
sum_view_emiss = sum(viewFactors[i] * emissivities[i] for i in range(len(viewFactors)))
for i, temp in enumerate(temperatures):
tempK = temp + 273.15
equRight = equRight + math.pow(tempK, 4) * viewFactors[i] * emissivities[i]
MRT = math.pow(equRight/sum_view_emiss, 0.25)
MRTC = MRT - 273.15
return MRTC

Hopefully i’ve interpreted what’s being discussed above correctly and the code is correct!

This used surface temps and the viewfactors from the UTCI component, and I also calculated a longwave delta between sensor and sky for outdoor sensors. For total MRT i added this customised longwave MRT to the UTCI shortwave MRT and sky delta. It’s a bit clumsy but gets me what i need.

Anyway, LBT has been a really great learning tool so big thanks for that!

1 Like
16

Thanks , @sineadn. Your code looks pretty good to me and effectively does what I was proposing above with an additional improvement that you’re also following the Stefan-Boltzmann Law by raising your values to the 4th power and then taking the 4th root. In honesty, I am not currently doing this n the LBT comfort maps because the 4th-power transformations really only make a meaningful difference when you have surface temperatures that are far apart from one another in their relation to absolute zero. So it’s very important for spacecraft. Not as important for UTCI mapping on Earth. But I will follow the law if I eventually do some emissivity weighting in the LBT comfort maps.

FYI, now that LBT 1.8 has a View Factors component, you should be able to do all of this type of custom comfort map building in LBT instead of Legacy.

I just know that there are some parts of Legacy that never worked correctly in Rhino 7 or 8 so you may have to stick to Rhino 6 along with some ancient versions of E+ to get everything to work. But, if you’re that deep into Legacy source code, I’m sure that you’re aware of anything that is not working correctly.

But just let me know and I’m happy to put together a LBT 1.8 sample of what I mean by doing custom thermal map building.

17

Hi Chris

“In honesty, I am not currently doing this n the LBT comfort maps because the 4th-power transformations really only make a meaningful difference when you have surface temperatures that are far apart from one another in their relation to absolute zero. So it’s very important for spacecraft. Not as important for UTCI mapping on Earth”

I can understand what you mean if i was looking at standard building materials, but i am for example comparing a photovoltaic shade material and an optimised shade material with very low emissivity, so their surface temperatures are quite different during the hottest parts of the day (>60°C), though i suppose that’s not that significant if we’re comparing with temperatures reached by spacecraft. But still, im getting about 10°c difference in MRT if the material is relatively close to the pedestrian - 2.4m, like a bus shelter.

I would quite like to see a LBT 1.8 sample for custom thermal mapping actually, if you’ve the time

Thanks again :slight_smile:

18

Hi @sineadn,

Thanks for pushing me to add the sample and sorry that it took me so long to get back to this. I know that a lot of people found the legacy sample for the deconstructed thermal map very helpful as an educational tool.

I just added it to the official set of regularly-updated example files:

And you can download it from here.

It has all of the different calculations that run under the hood of the thermal mapping recipes broken down into different sections:

image
image1774×609 77.8 KB

… and all ray tracing gets done using Rhino’s Mesh/Ray intersection (instead of Radiance) so that you can more easily play around with them in Grasshopper. Just be aware that the HB-Energy comfort mapping recipes use Radiance so they can model the shortwave solar reflections while this deconstructed example cannot.

You’ll see that you get a plot of PMV output from the whole process, for which you can scroll through the hours of the simulation:

image
image850×761 21.4 KB

If you want to play specifically with the effects of low-emissivity materials changing the longwave interaction with the occupants in the space, this is the part of the script that you should play around with:

image
image1178×514 50.9 KB

Instead of just multiplying temperatures by view factors and summing them, you can replace that with something more sophisticated.

Hope that helps!

3 Likes
19

Thank you very much Chris!

1 Like