Hello guys
I am working on a Heat Sink project. Anyone here was successful simulating heat/thermal phenomena like heat convection transfer inside Grasshopper? I am new to the FEA world and definitely lack the skills to replicate it inside Gh.
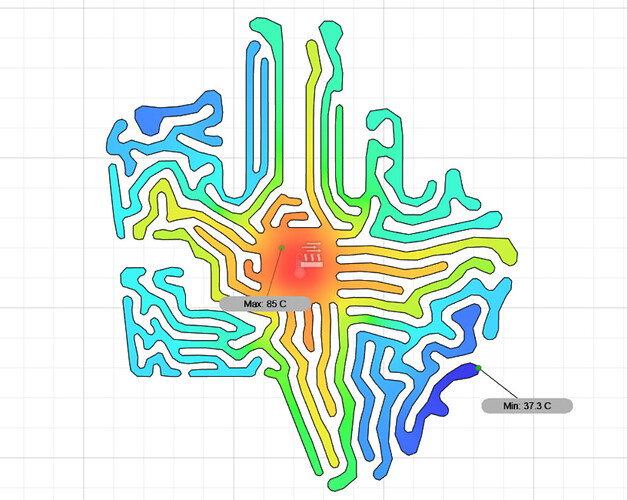
I am trying to simulate a 2D grid of cells with a heat source diffusing in a material. (I am designing a heat sink based upon generative algorithm) I am doing this step inside Fusion, but I am running an optimization loop, so I cannot manually do back and forth between Gh and Fusion 1000’s of times.
I tried to replicate this two dimensional heat conduction equation with Microsoft Excel Solver https://youtu.be/CSAIxrWu5nc?t=922 inside Grasshopper, but no luck so far. I am unable to find which algorithm the “Excel Solver” uses.
Is is possible to do this with Ladybug/Honeybee or DIVA etc, because as far as I know, you can only simulate solar radiation and not set certain portion of your geometry as a heat source.
It will be really helpful if you can point out any reference or articles that will help in replicating this inside Gh. For now even a rudimentary simple heat transfer system will also be a good step ahead.
Any help is appreciated.
1 Like
@creativemutation
You can definitely implement the simpler, 2D finite difference, heat equation (as shown in your video) in GH, I don’t think you need Ladybug for that.
However, the geometry you’re showing looks like it’s quite a bit more complicated then that. Specifically, your geometry will require modeling convective and radiative exchange between boundaries, involving the calculation of view factors and fluid exchange, respectively. Are you eventually going to model these components as well? It’s not as easy to calculate, and I think at that point it’d be easier to go to a specialized FEM tool, which is not available in Ladybug/Honeybee.
FYI, Ladybug tools does a lot more then just simulate solar radiation :), including building energy and thermal load simulation. It even supports 2D conduction heat transfer analysis (via the finite element method), through THERM, but it’s meant for envelope products, and doesn’t support the addition of a heat source.
1 Like
Thanks for the reply. Actually the starting geometry will be a simple rectangle, with the heat source at the center. The image can be considered as an end result of the algorithm (not an accurate depiction)
Regarding implementing the heat equation (Excel video) what I an unable to implement is the actual algorithm used by excel to calculate the variable cells. So the “Solver” part of the Excel is what I’m missing. Do you have any idea where can I get more info on that?
I need to run this inside GH because I’ll be running a genetic algorithm on top, and simulating it in Ansys or Fusion or Solid will be ideal but I’m unaware of creating a workflow between these softwares and GH.
If I can just run a simple 2D grid thermal simulation, with/without Ladybug, but inside Grasshopper will be enough for my use case! Thanks for the reply.
Also, is there anyway to contact you privately, to discuss if you will be interested in creating this simple 2D grid simulation?
Hi @creativemutation,
You can try to use Therm from Honeybee Legacy, as @SaeranVasanthakumar suggested. As Heat source you can use the Therm boundary. Here you can find some examples. Hydra - Sharing made easy!
1 Like
@Erikbeeren, @creativemutation
I actually didn’t think THERM would work here because @creativemutation is asking (and illustrating) a simulation with heat source at the center of a geometry. As far as I know, interior heat generation can’t be simulated with THERM. @creativemutation is the heat source in the center important?
Also, I’ll admit I’ve been assuming that the question was about a transient state simulation, which was the other reason I didn’t think THERM would work. However, if evolving temperature over time isn’t important, and having a constant heat source at the boundary is acceptable, I agree THERM is the best tool here.
1 Like
What I saw in the explanation of the excel example it was about a steady state calculation. Also the temperature input was constant and heat accumulation was set to 0. So I think Therm could do the job that @creativemutation was asking for.
@SaeranVasanthakumar @Erikbeeren
I am trying to replicate something similar to this heat sink design. There are 5 steps to this iterative process. https://www.edn.com/when-worlds-collide-heat-sink-design-3d-printing-dolly-the-sheep/
- Start with a minimal section of heatsink base.
- Simulate to model the temperature rise
- Where its surface is hottest, grow the geometry by a very small amount ( a full-length rod shape)
- Go to step 2
- Repeat until the available design space has been filled

I am trying to simulate a steady state heat transfer, where there is constant heat source at the center (CPU) and not at one of the sides. And loop it in an iterative process where we will first run the simulation, add a small part to the sheet metal where it was the hottest, than run the thermal simulation again, and so on.
@creativemutation creativemutation
A heat source in the center is not possible with Therm.
@creativemutation
I’ll explain how you can implement the 2D heat conduction calculation in GH. Broadly speaking, I think there are two ways to do it.
First option: Install an Excel to GH plugin and just implement the method described in your video. We probably should have mentioned this earlier, but I forgot this was an option. I don’t know if you can automate iterative runs with GH to Excel plugins, but if you can solve that this is likely the easiest solution.
Second option: Implement it in GH yourself. Fundamentally all you have to do is set up, and then solve a linear system of equations describing your 2D heat transfer.
The idea is since we know in a steady state system the rate of heat conduction (W) in and out is equal, we can set up an energy balance where all components sum to zero and discretize it:
\begin{align}
0 &= \frac{ \partial ^2T}{\partial x^2} + \frac{\partial ^2T}{ \partial y^2}\\
&= \frac{\frac{T_{left} - T_{center}}{\Delta{x}} - \frac{T_{center} - T_{right}}{\Delta{x}}}{\Delta{x}} -
\frac{\frac{T_{up} - T_{center}}{\Delta{y}} - \frac{T_{center} - T_{down}}{\Delta{y}}}{\Delta{y}}) \\
&= T_{left} + T_{right} + T_{up} + T_{down} - 4T_{center}\\
\end{align}
The ‘Solver’ in excel is simply identifying the best values for node temperatures that fit this equation. There many ways to do this, you can guess random values and iteratively update it, or solve it by inverting a matrix. I don’t know what Excel uses, but I think for the scale of your problem you can use an out-of-the-box matrix inversion method.
Implementing this in GH might be tricky, based on your comfort with math, and you’ll need access to a linear algebra library for some matrix operations. If you are willing to do it using CPython with Numpy (which requires a GH plugin), I am happy to share code. As you can see, it’s easy to implement if you stick to out-of-the-box matrix operations in Numpy:
Visualization:
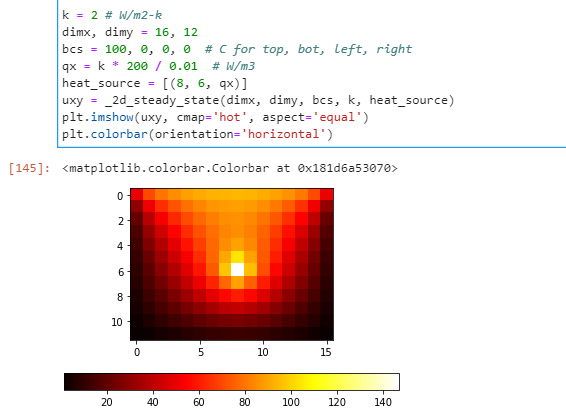
But, if you are more comfortable with Excel, I recommend using that first.