I’ll explain how you can implement the 2D heat conduction calculation in GH. Broadly speaking, I think there are two ways to do it.
First option: Install an Excel to GH plugin and just implement the method described in your video. We probably should have mentioned this earlier, but I forgot this was an option. I don’t know if you can automate iterative runs with GH to Excel plugins, but if you can solve that this is likely the easiest solution.
Second option: Implement it in GH yourself. Fundamentally all you have to do is set up, and then solve a linear system of equations describing your 2D heat transfer.
The idea is since we know in a steady state system the rate of heat conduction (W) in and out is equal, we can set up an energy balance where all components sum to zero and discretize it:
\begin{align}
0 &= \frac{ \partial ^2T}{\partial x^2} + \frac{\partial ^2T}{ \partial y^2}\\
&= \frac{\frac{T_{left} - T_{center}}{\Delta{x}} - \frac{T_{center} - T_{right}}{\Delta{x}}}{\Delta{x}} -
\frac{\frac{T_{up} - T_{center}}{\Delta{y}} - \frac{T_{center} - T_{down}}{\Delta{y}}}{\Delta{y}}) \\
&= T_{left} + T_{right} + T_{up} + T_{down} - 4T_{center}\\
\end{align}
The ‘Solver’ in excel is simply identifying the best values for node temperatures that fit this equation. There many ways to do this, you can guess random values and iteratively update it, or solve it by inverting a matrix. I don’t know what Excel uses, but I think for the scale of your problem you can use an out-of-the-box matrix inversion method.
Implementing this in GH might be tricky, based on your comfort with math, and you’ll need access to a linear algebra library for some matrix operations. If you are willing to do it using CPython with Numpy (which requires a GH plugin), I am happy to share code. As you can see, it’s easy to implement if you stick to out-of-the-box matrix operations in Numpy:
Visualization:
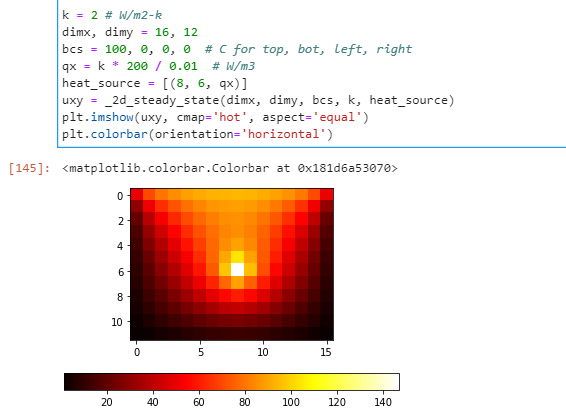
But, if you are more comfortable with Excel, I recommend using that first.
